Design Optimization of Sandwich Panels

The optimization of a composite plate is crucial analysis for layout of systems ranging from aircrafts to civil engineering structures. the design optimization hassle of present day interest is the minimization of the burden function for a sandwich composite plate. this is a design optimization problem which optimizes the thickness of the sandwich layers to give the minimal weight. of extra interest to contemporary have a look at are the works at the layout optimization of composite sandwich plates wherein the thickness of outer layers and the core are taken because the design variables.

SANDWICH THEORY The typical sandwich structure compounds of three layers. The outer layers are made of a material that has high strength (fiber reinforced laminates), which can transfer axial forces and bending moments, while the core is made of lightweight materials such as foam, alder wood etc. The material used in sandwich core must be resistant to compression and capable of transmitting shear. The thin cover sheets, i.e. the layers 1 and 3, have the thicknesses h1 for the lower skin and h3 for the upper skin. The thickness of the core is h2 (Fig. 1). In a general case, h1 does not have to be equal to h3, but in the most important practical case of symmetric sandwiches h1 = h3.

Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates.

For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix formwhere N, M, V are the vectors of normal forces,

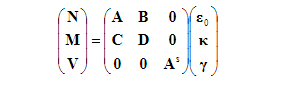
bending moments and transverse shear forces, respectively and γκε,,0are the vectors of mid-plane strains, curvatures and transverse shear strains, respectively. The stiffness coefficients are calculated aswhere E_i^s_j is the transverse shear modulus of the core.

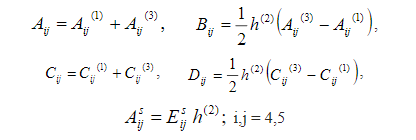
Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0

Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0

Most sandwich structures can be modeled and analyzed using the shear deformation theory for laminate plates [1-3]. For the resultants N and M the integration is carried out over the sheets only and for the transverse shear force over the core. The constitutive equations for a sandwich are written in the hypermatrix form γκεA000DC0BAVMNs0